语谱图的matlab提取和python提取

前言

语谱图（spectrogram或specgram），也叫声谱图，可以简单看做一个二维矩阵，其纵轴表示频率，横轴表示时间，矩阵的值表示能量强弱。由于它拥有着频率和时间两个维度的信息，所以是比较综合地表示原语音信息的一种特征。另外，我将其看做语音和图像的一种连接，因为图像领域的模型发展得较快，所以通过这种方式把语音转换成一种特殊的图像再进一步处理。

语谱图流程简介

1. 将语音可交叉地分成多帧（由于语音的短时平稳性）
2. 各帧加窗
3. 各帧通过快速傅里叶变化（fft）得到频谱向量
4. 沿着时间轴并联各频谱向量得到语谱图

语谱图的提取

语谱图的matlab提取

先看一段非官方代码，结合上述步骤进行理解。

[x,Fs,nBits]=wavread('audio.wav');

s=length(x);    % 信号长度
w=256;            % 窗长
n=w;            % nfft，表示做fft变换需要的点数，一般为刚大于w的2的幂。举例，w=250，则n一般设为256
ov=w/2;            % 分帧的交叉程度，常见设为窗长的二分之一或四分之一
h=w-ov;            % 不重叠点数
win=hamming(n)';% 选了常见的汉明窗，并设置nfft
c=1;            % 指向当前帧的指针
ncols=1+fix((s-n)/h);    % 计算总共有多少帧
d=zeros((1+n/2),ncols);    % 语谱图初始化

for b=0:h:(s-n)    % 以下处理各帧
    u=win.*x((b+1):(b+n));    % 各帧加窗
    t=fft(u,n);                % 各帧进行fft，内容为u，nfft=n。对于fft，输入n个时域点，输出n个频域点
    d(:,c)=t(1:(1+n/2))';    % 并联频谱向量，注意只取1+n/2，因为负频率无意义，只留下0和正频率
    c=c+1;        % 移动指针
end
tt=[0:h:(s-n)]/Fs;    % 时间轴
ff=[0:(n/2)]*Fs/n;    % 频率轴

imagesc(tt/1000,ff/1000,20*log10(abs(d)));    % 绘制
colormap(hot);
axis xy
xlabel('时间/s');
ylabel('频率/kHz');

然而，matlab其实有封装好的函数可以直接调用。

[S,F,T]=specgram(x,nfft,Fs,windows_length,overlap_length)
% x 为整段语音
% nfft 为fft变换点数，其实可以直接用默认的刚大于窗长的2的幂。也可自定义为大于窗长的整数，会对帧进行补零操作
% Fs 语音采样频率
% windows_length 窗长
% overlap_length 交叉长度
% S 语谱图
% F 频率值，尺度为1+n/2
% T 时间值，尺度为1+fix((s-n)/h)

语谱图的python提取

有了刚才的基础，python的代码就容易理解啦。首先同样看一下不直接调用函数的写法。

import numpy as np
from scipy.io import wavfile
import matplotlib.pyplot as plt

Fs, x =  wavfile.read('audio.wav')
wave = np.array(x[:,0], dtype = "float")

frame_len = 1000
frame_off = frame_len // 2    # 非重叠点数
specg_len = 1024

# 可以想象1是代表第一帧，然后第二帧结尾超出第一帧frame_off个点，第三帧再超出第二帧frame_off个点，总共第二帧到最后一帧共有(wave.size - frame_len) // frame_off 帧
frame_num = (wave.size - frame_len) // frame_off + 1
# 生成汉明窗
hamwindow = np.hamming(frame_len)
specg = np.zeros((frame_num, specg_len // 2 + 1))
z = np.zeros(specg_len - frame_len)

for idx in range(frame_num):
    base = idx * frame_off
    frame = wave[base: base + frame_len]            # 分帧
    frame = np.append(frame * hamwindow, z)         # 加窗
    specg[idx:] = np.log10(np.abs(np.fft.rfft(frame))) # FFT，返回幅度谱

specg = np.transpose(specg)
io.savemat('specgram.mat', {'specg':specg})

# aspect设为auto即可自动拉宽图
plt.imshow(specg, origin="lower", cmap = "jet", aspect = "auto", interpolation = "none")
plt.show()
plt.xticks([])
plt.yticks([])
plt.savefig('specgram.png',bbox_inches='tight',pad_inches=0.0)
plt.close()

再看看已经封装好的版本。

from scipy import io
from scipy.io import wavfile
import matplotlib.pyplot as plt

Fs, x = wavfile.read('audio.wav')    # 读取音频
specg = plt.specgram(x, Fs = Fs, pad_to = 256, NFFT = 256, noverlap = 128)    # 提取语谱图，一键操作！
io.savemat('specgram.mat', {'specg':specg[0]})    # 保存语谱图
## 照例解释下参数
# x，Fs和上边一样
# pad_to为上边的nfft
# NFFT为上边的windows_length（为什么nfft不设置为上边的nfft呢，迷惑）
# noverlap为上边的overlap_length

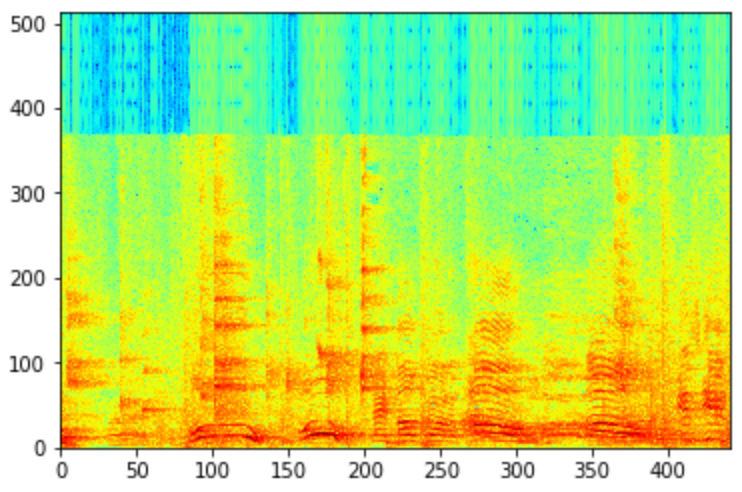
这里补充一点，语谱图根据带通滤波器的宽窄，可分为宽带语谱图和窄带语谱图。上图为窄带语谱图。
窄带语谱图，频率轴的分辨率较细，反映频谱的精细结构，可以看到很多“横杠”，“横杠”之间的距离就是基音频率；
宽带语谱图，频率轴的分辨率较粗，反映频谱的快速时变过程，可以看到很多细竖条，这些细条之间的距离就是基音周期。

补充一个librosa版本

librosa提取的是梅尔频谱图，即在频谱图基础上再进一步将各帧通过梅尔滤波器(还可加对数操作)。另外若是在此基础上再进行倒谱即获得MFCC。
还要注意到，梅尔频谱图的输出尺寸，频率等于梅尔滤波器的个数n_mels, 时间则只取决于窗移(非重叠数)hop_length(还没想明白，推测可能是进行了填充，所以尺寸上忽视了窗长的影响)。
此外，还可通过设置power参数来确定要计算梅尔频谱图(设置为1)还是梅尔功率图(设置为2)。

from matplotlib import pyplot as plt
import librosa
import librosa.display


# Load a wav file
y, sr = librosa.load('./test.wav', sr=None)
# plot a wavform
plt.figure()
librosa.display.waveplot(y, sr)
# plt.plot(y)
plt.title('wavform')
plt.show()

# extract mel spectrogram feature
melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, win_length=1024, hop_length=512, n_mels=128, power=2.0)
# convert to log scale
logmelspec = librosa.power_to_db(melspec)
# plot mel spectrogram
plt.figure()
librosa.display.specshow(logmelspec, sr=sr, x_axis='time', y_axis='mel')
plt.title('spectrogram')
plt.show()

# aspect设为auto即可自动拉宽图
plt.imshow(logmelspec, origin="lower", cmap = "jet", aspect = "auto", interpolation = "none")
plt.show()
plt.xticks([])
plt.yticks([])
plt.savefig('specgram.png',bbox_inches='tight',pad_inches=0.0)
plt.close()

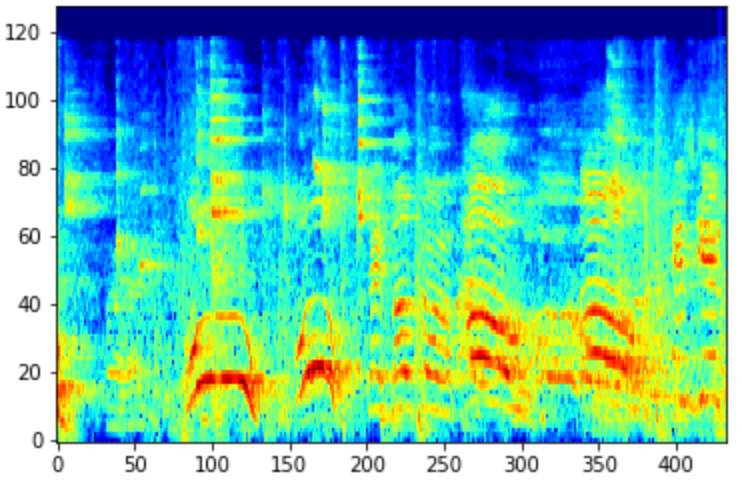
下图中，第一张是梅尔频谱图，第二张是梅尔功率图，功率图的声音和噪声区分更明显。而两者都比没有梅尔滤波器的频谱图有更独特明显的能量显示。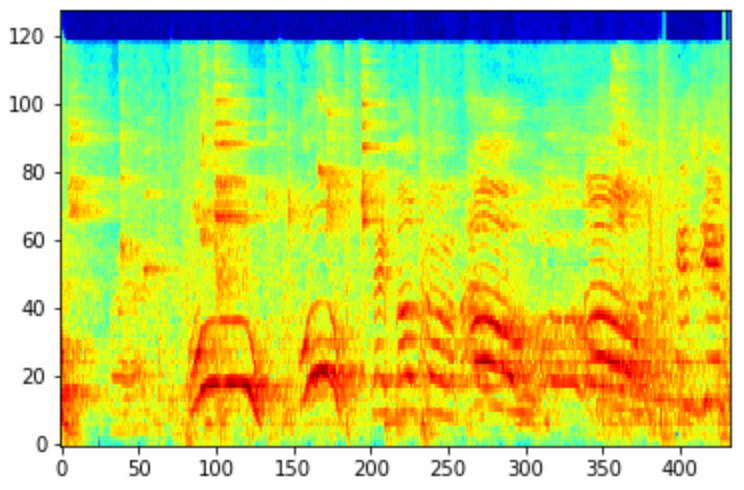

语谱图的一些可能有的小疑惑

1. 关于nfft
   nfft既表示时域的点数也关联频域的点数。该数为2的幂数时更高效，但不是也没问题。
   nfft需要比窗长的值更大，然后加窗后的帧会被补零到nfft长度再进行fft。
2. 关于频率分辨率
   频率轴上每一个点对应fs/nfft的频率。另外由于输出nfft/2+1个频率点，所以输出的频率范围为0到nfft/2×fs/nfft=fs/2。
3. 关于自定义输出语谱图的尺寸问题
   时间轴尺寸为1+fix((s-n)/h)， 由windows_length和overlap_length决定。实际应用时由于各语音长度不同，时间尺寸一般都要进行截断或补零到一个固定值。截断的话可以截一段（起始信息，中间信息），也可以截多段（交叉不交叉都行）。
   频率轴尺寸为1+n/2，仅决定于nfft（python中的pad_to参数），所以可以通过设置该值控制频率轴尺寸。但是也不要比窗长大太多，否则补零太多可能就没什么信息了。nfft调大时，窗长可以跟着调大，为了防止导致的时间轴太短可以调高overlap_length。
   另外，其他参数不变时，仅变换nfft，可视化出来时可能肉眼看起来一样，但实际分辨率仍然是不同的。这也导致了一个问题，送入网络的是要用单通道的直接计算出来的语谱图，还是用可视化函数绘制出来的三通道的语谱图，这就根据实际情况去尝试了。

彩蛋

希望疫情早点过去